9063. Древнегреческая
машина
После
долгих путешествий и скитаний, в одном храме Кратос обнаружил интересную
находку – дневнегреческую машину. Это был один из первых прототипов, который
работал на чистой энергии. В этом же храме Кратос нашел и топливо – фонтан,
содержащий a литров чистой
энергии.
Кратос
знает, что 1 литра чистой энергии достаточно для преодоления 100 километров.
Однако, есть одна проблема – бак машины рассчитан так, что в него помещается не
более 1 литра энергии, а пополнять энергию можно только в храме. Однако,
внимательно изучив структуру этой чистой энергии, Кратос понял, что в любом
месте своего пути сможет слить ее и оставить на земле, а затем вернуться и
дозалить в бак без потерь. Теперь его интересует вопрос – какое максимальное
расстояние он может проехать на найденной машине?
Вход. Одно вещественное
число а (0.0 ≤ a ≤ 2.0) –
количество литров чистой энергии в фонтане.
Выход. Выведите максимальное расстояние, которое Кратос может
проехать на найденной машине. Ответ следует выводить с точностью до 6 десятичных
знаков.
|
Пример
входа |
Пример
выхода |
|
1.000000 |
100 |
РЕШЕНИЕ
математика
Анализ алгоритма
На 1 литре
чистой энергии можно проехать 100 километров. Если в наличии имеется a ≤ 1.0 литров энергии,
то максимум можно преодолеть 100a километров, залив всю энергию
в бак изначально.
Рассмотрим случай 1.0 < a ≤ 2.0. Пусть в бак изначально будет
залит 1 литр энергии. Машина поехала вперед, потратила x литров, оставила на земле (1 – 2x) литров и вернулась назад, потратив последние взятые с собой x литров.
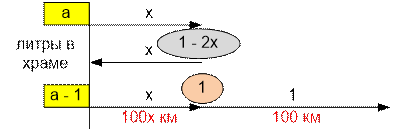
В храме осталось a – 1 литров энергии, Кратос заливает их в бак. Доехав до места, где осталась
неиспользованная энергия, и использовав при этом x литров, он должен забрать ее
всю, наполнив бак до 1. В этом случае он доедет максимально дальше, потратив
всю находящуюся в наличии энергию. Когда Кратос доедет
до оставленной на земле энергии, в баке у него будет (a – 1 – x)
литров топлива.
Добавив оставленную на земле энергию (1 – 2x), бак должен наполниться до конца. Должно выполнять
условие: (a – 1 – x) + (1 – 2x) = 1. Решаем уравнение: a – 3x = 1,
или x = (a – 1) / 3. Машина Кратоса
проедет максимум
100x + 100 = 100 * (a – 1) / 3 + 100
километров.
Реализация алгоритма
Читаем входные данные.
scanf("%lf", &a);
Вычисляем результат res в
зависимости от значения a.
if (a <= 1)
res = 100 * a;
else
res = 100 + 100 * (a - 1) / 3;
Выводим ответ.
printf("%.6lf\n", res);